How is RSA used for x509 certificate signing?
Having worked a fair bit with certificates in other posts, I’ve been aware that I’ve been accepting that certificate signatures work without getting under the covers of specifically how these signatures are generated and validated.
In this post, I aim to explore the use of RSA for certificate signing and verification - in particular the sha256WithRSAEncryption signature algorithm which was the default openssl signing method used when I created my dummyCA within this post.
I need to acknowledge this blog post up-front - it was invaluable in helping grasp the mechanisms used as part of signature verification - I’m replicating much of that post here but taking some differing approaches (use of python throughout, and use of a dummyCA to explore the signing process).
Questions to explore
To further understanding, I’d like to explore the following questions and where applicable demonstrate answers:
- What underlying mathematics operations take place to RSA sign an x509 certificate?
- which parts of an x509 certificate are signed?
- when the hash/digest of a certificate is generated, is this the only part signed?
- Similarly, what operations take place when a client verifies the signature of an x509 certificate?
- Which standards/rfcs define the signing processes?
- Can I re-create the signing and verification processes by hand, down to the mathematic operations?
DummyCA recap
As outlined above, I’m re-using the dummyCA created in this post - steps below.
1
2
3
4
5
6
$ cd ~/dummyCA/
$ openssl req -x509 -nodes -newkey rsa:2048 -keyout dummyCA.key \
-sha256 -days 365 -out dummyCA.pem \
-subj "/CN=dummyCA/"
$ ls
dummyCA.key dummyCA.pem
Expand for full `-text` openssl output of this cert
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
$ openssl x509 -in dummyCA.pem -text -noout
Certificate:
Data:
Version: 3 (0x2)
Serial Number:
3e:44:4c:e5:37:d0:56:4b:2a:ac:4b:4e:77:e5:f2:e2:69:64:27:14
Signature Algorithm: sha256WithRSAEncryption
Issuer: CN = dummyCA
Validity
Not Before: Dec 8 17:16:03 2024 GMT
Not After : Dec 8 17:16:03 2025 GMT
Subject: CN = dummyCA
Subject Public Key Info:
Public Key Algorithm: rsaEncryption
Public-Key: (2048 bit)
Modulus:
00:a2:79:0d:9e:1a:a9:82:4d:cc:33:3f:db:bc:43:
ab:64:e1:9b:3e:f3:92:d0:da:18:e0:8c:8e:73:e8:
b0:93:a7:d7:ae:df:d8:92:29:d4:a0:50:ca:5e:2e:
c5:6e:6f:c8:35:89:80:b0:a7:9d:53:2d:64:24:35:
08:91:e0:99:77:48:2e:da:93:f0:ea:25:3c:5c:de:
a8:a2:d5:e6:b2:f3:a1:15:68:ce:a4:37:26:cf:bb:
ba:43:02:d5:ac:7f:a2:43:3c:8e:fb:19:89:05:49:
55:07:59:5c:79:b1:b4:51:f8:d1:d4:b3:87:73:bd:
b3:9a:9c:e2:8e:b5:76:d5:0b:b5:3f:df:4b:cf:4b:
2f:2d:ad:fc:7e:0a:e7:b9:79:ea:20:ec:ca:b6:0b:
83:ed:20:e4:1a:18:83:19:f5:73:12:00:5f:a8:7b:
b6:f7:18:86:3a:31:d3:39:37:d3:ac:37:0d:ea:f0:
33:1e:dc:e1:74:61:8b:50:70:7c:09:60:d4:8f:54:
68:c5:a6:4a:1d:d9:c6:05:a7:95:ac:e2:5c:f4:59:
a7:61:86:26:63:0a:4f:6e:39:76:d4:a1:34:e7:5c:
83:03:d0:a6:fd:27:65:78:a4:27:91:0e:bb:75:00:
f9:40:23:32:d1:48:c7:6d:31:9c:0e:9a:98:88:e2:
68:9f
Exponent: 65537 (0x10001)
X509v3 extensions:
X509v3 Subject Key Identifier:
3A:1A:83:4F:F4:57:F3:E4:39:9C:33:00:48:76:8F:64:67:92:78:40
X509v3 Authority Key Identifier:
3A:1A:83:4F:F4:57:F3:E4:39:9C:33:00:48:76:8F:64:67:92:78:40
X509v3 Basic Constraints: critical
CA:TRUE
Signature Algorithm: sha256WithRSAEncryption
Signature Value:
74:10:4c:69:6d:25:47:2f:96:0f:75:79:9b:cc:41:a8:47:7d:
69:33:5f:9a:94:c0:44:b9:60:b9:30:fe:d5:5d:0e:1e:40:bd:
13:5b:0a:d3:ae:38:21:8c:2b:30:5f:59:51:f9:04:57:4b:48:
4f:e7:1f:6b:a6:85:44:5b:32:29:20:9a:2e:97:17:81:68:6f:
7b:a2:48:54:05:2d:74:12:b0:f0:72:fd:39:07:a7:b4:b9:bd:
c5:61:cd:21:3f:9e:5c:c9:58:f1:a5:a2:91:97:a9:44:36:2c:
6c:67:50:e6:ac:d2:dd:45:96:77:a7:62:91:2e:cf:cd:6a:b1:
b4:71:8b:a2:32:45:0e:9c:aa:bc:e7:e6:09:84:04:43:7e:3f:
46:43:0f:4b:99:f8:80:d1:4f:d1:b4:b7:f0:1a:a2:d8:76:c5:
e2:57:75:eb:82:a1:f3:73:d3:77:40:e4:a3:74:99:8c:5f:ec:
e0:d4:52:d7:b4:a5:89:bf:ed:5c:13:b4:8e:f9:a6:02:c7:f9:
5a:f4:4a:6f:e5:5b:8e:d0:50:27:3a:98:f3:eb:07:a5:ef:9c:
16:0d:a8:40:d0:91:3e:1a:4e:c7:a1:27:66:42:12:11:11:ec:
6d:4c:74:d1:02:57:d2:a6:04:98:51:6a:f1:66:13:a5:0b:8c:
21:fd:12:38
I’m also going to use (and show) the values of the private key - this is all for demonstration purposes so there are no issues in sharing this private key here…
Expand for full `-text` openssl output of this private key
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
$ openssl rsa -in CA-key.key -text
Private-Key: (2048 bit, 2 primes)
modulus:
00:a2:79:0d:9e:1a:a9:82:4d:cc:33:3f:db:bc:43:
ab:64:e1:9b:3e:f3:92:d0:da:18:e0:8c:8e:73:e8:
b0:93:a7:d7:ae:df:d8:92:29:d4:a0:50:ca:5e:2e:
c5:6e:6f:c8:35:89:80:b0:a7:9d:53:2d:64:24:35:
08:91:e0:99:77:48:2e:da:93:f0:ea:25:3c:5c:de:
a8:a2:d5:e6:b2:f3:a1:15:68:ce:a4:37:26:cf:bb:
ba:43:02:d5:ac:7f:a2:43:3c:8e:fb:19:89:05:49:
55:07:59:5c:79:b1:b4:51:f8:d1:d4:b3:87:73:bd:
b3:9a:9c:e2:8e:b5:76:d5:0b:b5:3f:df:4b:cf:4b:
2f:2d:ad:fc:7e:0a:e7:b9:79:ea:20:ec:ca:b6:0b:
83:ed:20:e4:1a:18:83:19:f5:73:12:00:5f:a8:7b:
b6:f7:18:86:3a:31:d3:39:37:d3:ac:37:0d:ea:f0:
33:1e:dc:e1:74:61:8b:50:70:7c:09:60:d4:8f:54:
68:c5:a6:4a:1d:d9:c6:05:a7:95:ac:e2:5c:f4:59:
a7:61:86:26:63:0a:4f:6e:39:76:d4:a1:34:e7:5c:
83:03:d0:a6:fd:27:65:78:a4:27:91:0e:bb:75:00:
f9:40:23:32:d1:48:c7:6d:31:9c:0e:9a:98:88:e2:
68:9f
publicExponent: 65537 (0x10001)
privateExponent:
0d:27:43:1f:11:59:50:ca:95:65:3e:c4:f1:a2:02:
0b:4d:0f:47:c5:b6:95:66:f4:58:d5:85:0d:ab:67:
9d:d1:67:7b:cf:f4:e2:0f:9c:4b:40:4f:29:d8:35:
b5:08:6f:7e:7a:15:6b:91:6b:1b:e6:df:8c:4c:0f:
3e:0d:b8:f5:51:b5:00:8e:82:94:70:93:7c:90:e0:
1f:92:b5:03:1e:d4:ca:63:d3:e1:4c:26:24:22:36:
7e:6f:56:36:ef:c9:1f:de:fa:ba:5a:cf:f9:18:17:
3e:43:2b:48:b8:13:2c:6e:86:f3:e6:43:b6:22:2a:
9b:18:81:68:2f:b0:87:a7:65:83:48:41:df:96:1e:
22:f0:d5:fe:24:01:4b:b6:f0:26:0c:f7:61:64:c5:
8f:f1:af:99:aa:65:29:06:3f:7c:f7:f5:04:60:d6:
75:d9:c4:76:dd:2c:64:4f:e7:b6:11:5f:53:64:1d:
2c:7a:ca:d8:71:9f:af:4b:93:fd:05:ce:89:7d:fd:
32:99:94:d0:4c:76:aa:c3:91:d7:a3:0a:ae:65:6f:
25:68:a9:a8:fa:fc:8c:b1:b7:69:f7:e3:ba:4f:13:
8e:e0:67:6b:81:be:98:11:54:03:c6:e5:47:07:9b:
b9:7a:c4:93:c3:87:cc:3f:e4:c7:89:9b:33:93:a9:
01
prime1:
00:e1:53:ef:a5:c4:ab:8d:0a:43:b7:2d:02:15:11:
09:8d:46:b9:f2:48:49:09:51:92:d0:59:75:99:76:
50:34:bf:0e:5c:4d:24:25:a0:77:a3:23:f2:af:75:
77:5c:10:7c:97:29:00:9f:88:24:70:b1:74:ac:27:
b1:5c:29:97:b4:b3:21:8a:9b:1d:a7:3f:db:8f:7a:
b7:eb:8b:92:5d:e3:6d:3f:77:e0:c9:71:ca:16:cd:
b2:60:0c:25:f9:bd:68:82:f2:58:c3:fd:e7:37:c2:
e5:6d:ef:c3:81:ae:d3:ed:f9:ef:35:a4:c7:c9:f1:
95:9a:59:e9:5c:1f:4e:63:01
prime2:
00:b8:96:ca:71:f6:92:40:a5:7a:a8:e0:70:39:c6:
e3:4a:88:48:ac:16:c4:6a:77:9d:b6:7c:d2:3c:29:
07:01:c9:ec:3f:78:42:ad:ae:56:01:d5:c9:a3:7c:
e8:10:9b:03:db:76:3e:81:6c:45:92:0c:1f:3b:d2:
86:8f:d4:1e:78:92:98:ce:5c:27:b1:10:32:bf:d2:
80:ee:37:23:00:9a:7b:c3:a5:f8:57:0f:02:5b:c2:
41:8e:37:92:6e:0d:a0:17:1d:5d:1f:62:e1:06:52:
a8:62:df:1a:02:10:3e:c5:f6:b4:ed:f4:4a:d1:21:
e6:0a:41:14:c9:cf:51:eb:9f
exponent1:
51:e3:f9:72:9b:79:65:76:d7:89:58:f8:2a:c3:d8:
5e:d9:d7:76:70:42:ea:fa:14:8b:58:17:df:40:1a:
82:30:f5:7d:22:24:02:f0:c0:ca:2f:a4:61:94:25:
5e:f6:36:f1:90:db:43:1f:6d:6e:ef:6f:61:a9:c3:
51:a5:64:17:2e:0b:00:9e:c3:36:27:85:1a:2e:15:
6d:ab:79:f4:59:55:38:fd:ce:5a:27:da:b4:52:e9:
82:f2:a7:52:8e:3d:cf:69:58:4d:52:97:97:b2:63:
43:83:21:e0:9d:b3:34:07:e3:a1:f1:53:12:d7:93:
f1:56:bf:f2:d5:05:de:01
exponent2:
00:b0:f2:9c:0e:b3:37:70:11:31:8c:41:da:53:08:
7d:4a:2d:6a:bc:cc:f6:6c:b9:4d:ce:69:c9:7f:32:
35:2d:59:cb:c6:ec:19:bf:34:a7:ee:0a:6a:c8:f6:
2b:df:ff:39:ab:5f:a6:7b:9a:b6:f6:51:f8:7e:f8:
49:56:07:19:4e:ab:f9:1f:98:e7:d3:ac:9b:79:96:
e9:51:72:39:73:92:a3:a1:e1:b0:36:84:84:d6:41:
59:66:63:8f:53:40:6c:7e:bb:ff:50:df:10:a7:67:
05:54:02:5a:84:2f:de:7d:17:0a:4a:31:2c:a7:5d:
bf:8f:84:e3:d0:b1:94:ee:31
coefficient:
07:07:37:7f:f0:da:75:33:45:cf:ed:9a:f9:dc:a9:
8e:dd:80:f5:02:f7:a4:d3:10:76:9b:dc:c1:25:b5:
31:6b:37:08:8a:3d:97:fa:ac:07:2c:90:58:8f:14:
c8:7c:f4:81:7d:e8:43:24:03:7a:b7:69:0b:19:c8:
c8:57:20:36:15:87:87:14:97:9c:cb:70:3b:f4:06:
c8:9d:30:cb:3a:60:8d:16:0b:60:a8:ff:25:d0:22:
f0:42:a1:26:50:ea:f9:f7:9c:88:a6:05:5e:67:77:
14:5e:a3:ed:1a:a8:1e:0d:e2:74:98:2b:09:23:51:
52:60:4e:22:2a:cb:f1:64
writing RSA key
-----BEGIN PRIVATE KEY-----
MIIEvQIBADANBgkqhkiG9w0BAQEFAASCBKcwggSjAgEAAoIBAQCieQ2eGqmCTcwz
P9u8Q6tk4Zs+85LQ2hjgjI5z6LCTp9eu39iSKdSgUMpeLsVub8g1iYCwp51TLWQk
NQiR4Jl3SC7ak/DqJTxc3qii1eay86EVaM6kNybPu7pDAtWsf6JDPI77GYkFSVUH
WVx5sbRR+NHUs4dzvbOanOKOtXbVC7U/30vPSy8trfx+Cue5eeog7Mq2C4PtIOQa
GIMZ9XMSAF+oe7b3GIY6MdM5N9OsNw3q8DMe3OF0YYtQcHwJYNSPVGjFpkod2cYF
p5Ws4lz0WadhhiZjCk9uOXbUoTTnXIMD0Kb9J2V4pCeRDrt1APlAIzLRSMdtMZwO
mpiI4mifAgMBAAECggEADSdDHxFZUMqVZT7E8aICC00PR8W2lWb0WNWFDatnndFn
e8/04g+cS0BPKdg1tQhvfnoVa5FrG+bfjEwPPg249VG1AI6ClHCTfJDgH5K1Ax7U
ymPT4UwmJCI2fm9WNu/JH976ulrP+RgXPkMrSLgTLG6G8+ZDtiIqmxiBaC+wh6dl
g0hB35YeIvDV/iQBS7bwJgz3YWTFj/GvmaplKQY/fPf1BGDWddnEdt0sZE/nthFf
U2QdLHrK2HGfr0uT/QXOiX39MpmU0Ex2qsOR16MKrmVvJWipqPr8jLG3affjuk8T
juBna4G+mBFUA8blRwebuXrEk8OHzD/kx4mbM5OpAQKBgQDhU++lxKuNCkO3LQIV
EQmNRrnySEkJUZLQWXWZdlA0vw5cTSQloHejI/KvdXdcEHyXKQCfiCRwsXSsJ7Fc
KZe0syGKmx2nP9uPerfri5Jd420/d+DJccoWzbJgDCX5vWiC8ljD/ec3wuVt78OB
rtPt+e81pMfJ8ZWaWelcH05jAQKBgQC4lspx9pJApXqo4HA5xuNKiEisFsRqd522
fNI8KQcByew/eEKtrlYB1cmjfOgQmwPbdj6BbEWSDB870oaP1B54kpjOXCexEDK/
0oDuNyMAmnvDpfhXDwJbwkGON5JuDaAXHV0fYuEGUqhi3xoCED7F9rTt9ErRIeYK
QRTJz1HrnwKBgFHj+XKbeWV214lY+CrD2F7Z13ZwQur6FItYF99AGoIw9X0iJALw
wMovpGGUJV72NvGQ20MfbW7vb2Gpw1GlZBcuCwCewzYnhRouFW2refRZVTj9zlon
2rRS6YLyp1KOPc9pWE1Sl5eyY0ODIeCdszQH46HxUxLXk/FWv/LVBd4BAoGBALDy
nA6zN3ARMYxB2lMIfUotarzM9my5Tc5pyX8yNS1Zy8bsGb80p+4Kasj2K9//Oatf
pnuatvZR+H74SVYHGU6r+R+Y59Osm3mW6VFyOXOSo6HhsDaEhNZBWWZjj1NAbH67
/1DfEKdnBVQCWoQv3n0XCkoxLKddv4+E49CxlO4xAoGABwc3f/DadTNFz+2a+dyp
jt2A9QL3pNMQdpvcwSW1MWs3CIo9l/qsByyQWI8UyHz0gX3oQyQDerdpCxnIyFcg
NhWHhxSXnMtwO/QGyJ0wyzpgjRYLYKj/JdAi8EKhJlDq+feciKYFXmd3FF6j7Rqo
Hg3idJgrCSNRUmBOIirL8WQ=
-----END PRIVATE KEY-----
Additionally the steps for creating an end-entity CSR….
1
2
$ openssl req -nodes -newkey rsa:2048 -keyout end-entity.key \
-out end-entity.csr -subj "/CN=end-entity/"
Expand for full `-text` openssl output of this CSR
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
$ openssl req -in end-entity.csr -noout -text
Certificate Request:
Data:
Version: 1 (0x0)
Subject: CN = end-entity
Subject Public Key Info:
Public Key Algorithm: rsaEncryption
Public-Key: (2048 bit)
Modulus:
00:b9:3a:98:e4:73:d8:4b:be:66:9a:d5:15:de:bd:
41:aa:76:cd:2e:4f:b9:e2:5d:1e:6b:f0:de:7c:9f:
38:14:4b:52:56:3b:15:ac:aa:59:74:68:f8:d5:0b:
d4:36:7e:84:e8:b1:0d:16:9a:3d:10:6b:84:5b:ec:
13:56:46:06:1b:2f:54:9f:a0:d0:43:96:a3:d3:40:
9f:de:7d:6d:c9:46:c5:56:28:b1:d0:1c:2d:a1:74:
40:4a:6b:f1:b8:62:7a:05:d3:c9:b3:67:4e:09:84:
bf:24:a7:57:97:d0:10:09:20:38:f6:7a:10:6c:19:
de:5e:25:0a:cf:00:76:7d:b2:e8:79:6e:62:94:99:
ec:15:7b:b6:7d:39:4e:cd:ed:68:06:93:db:7f:b1:
36:5d:c2:b1:d6:71:b7:15:65:9d:51:cb:be:43:0c:
cd:c7:77:bb:d9:72:2b:4a:ab:c4:0b:fd:21:a9:49:
d6:53:a3:1d:40:39:a5:0c:05:c5:a9:d9:36:d7:17:
05:5d:9d:72:32:14:fc:66:3d:b5:09:42:fb:49:49:
8f:8e:89:c0:2b:60:f1:bc:79:b5:62:80:79:35:f2:
2c:11:f4:03:41:6a:f8:65:8c:63:53:c7:b2:b8:df:
2f:f9:d4:14:c0:e2:a9:b1:6c:8a:ce:61:72:04:d4:
b9:27
Exponent: 65537 (0x10001)
Attributes:
(none)
Requested Extensions:
Signature Algorithm: sha256WithRSAEncryption
Signature Value:
19:e4:ea:13:69:1e:cb:51:9a:e5:a4:9c:b4:dc:2b:bd:c7:1b:
f6:5e:9c:f9:b9:75:65:9b:53:d2:c7:6f:96:d7:3b:b7:93:09:
91:d7:50:20:3e:32:38:3c:f8:36:96:73:b0:64:a6:9a:ae:f4:
15:4c:9d:e5:df:7a:98:d3:65:85:e2:ba:77:06:08:a9:c6:fa:
25:7b:0e:95:76:39:fc:76:aa:be:c6:82:b3:c9:a5:63:bc:3a:
38:48:d2:c6:42:8f:be:3a:c7:7b:03:a1:3c:b5:24:90:99:20:
7a:10:26:05:26:b3:09:be:31:74:1d:1a:8c:23:f5:b6:ee:55:
87:24:a8:87:c9:02:84:7e:62:6a:e7:d2:95:80:06:30:fc:f8:
cd:14:ca:d5:11:47:ca:68:3a:ad:51:13:74:9d:53:43:b1:ef:
98:af:6e:c9:1f:5b:88:c5:41:97:94:e8:36:45:fe:ef:d5:9b:
8b:40:30:c8:09:9b:a8:e6:b6:6a:83:2d:24:ac:08:69:99:d5:
2f:22:3d:f8:d1:6a:45:ad:41:f6:6d:7d:3d:fd:f0:ca:ee:31:
28:1a:ea:86:3b:93:1d:33:fc:66:d0:6e:76:d2:24:e5:76:57:
5c:fc:5b:1d:50:67:9e:8d:99:b9:88:e0:39:90:59:34:ab:7e:
83:b7:8a:c0
… and generating a signed cert from that CSR …
1
2
3
4
5
6
7
8
$ cat v3.ext
authorityKeyIdentifier = keyid,issuer
basicConstraints = critical, CA:FALSE
keyUsage = digitalSignature
$ openssl x509 -req -in end-entity.csr -CA dummyCA.pem -CAkey dummyCA.key \
-CAcreateserial -out end-entity.pem -days 364 -sha256 -extfile v3.ext
Certificate request self-signature ok
subject=CN = end-entity
Expand for full `-text` openssl output of this signed certificate
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
$ openssl x509 -in end-entity.pem -text -noout
Certificate:
Data:
Version: 3 (0x2)
Serial Number:
12:c8:b2:0b:cb:e3:4e:a7:3e:a7:12:8f:f2:79:98:e2:df:6f:72:83
Signature Algorithm: sha256WithRSAEncryption
Issuer: CN = dummyCA
Validity
Not Before: Dec 8 18:10:54 2024 GMT
Not After : Dec 7 18:10:54 2025 GMT
Subject: CN = end-entity
Subject Public Key Info:
Public Key Algorithm: rsaEncryption
Public-Key: (2048 bit)
Modulus:
00:b9:3a:98:e4:73:d8:4b:be:66:9a:d5:15:de:bd:
41:aa:76:cd:2e:4f:b9:e2:5d:1e:6b:f0:de:7c:9f:
38:14:4b:52:56:3b:15:ac:aa:59:74:68:f8:d5:0b:
d4:36:7e:84:e8:b1:0d:16:9a:3d:10:6b:84:5b:ec:
13:56:46:06:1b:2f:54:9f:a0:d0:43:96:a3:d3:40:
9f:de:7d:6d:c9:46:c5:56:28:b1:d0:1c:2d:a1:74:
40:4a:6b:f1:b8:62:7a:05:d3:c9:b3:67:4e:09:84:
bf:24:a7:57:97:d0:10:09:20:38:f6:7a:10:6c:19:
de:5e:25:0a:cf:00:76:7d:b2:e8:79:6e:62:94:99:
ec:15:7b:b6:7d:39:4e:cd:ed:68:06:93:db:7f:b1:
36:5d:c2:b1:d6:71:b7:15:65:9d:51:cb:be:43:0c:
cd:c7:77:bb:d9:72:2b:4a:ab:c4:0b:fd:21:a9:49:
d6:53:a3:1d:40:39:a5:0c:05:c5:a9:d9:36:d7:17:
05:5d:9d:72:32:14:fc:66:3d:b5:09:42:fb:49:49:
8f:8e:89:c0:2b:60:f1:bc:79:b5:62:80:79:35:f2:
2c:11:f4:03:41:6a:f8:65:8c:63:53:c7:b2:b8:df:
2f:f9:d4:14:c0:e2:a9:b1:6c:8a:ce:61:72:04:d4:
b9:27
Exponent: 65537 (0x10001)
X509v3 extensions:
X509v3 Authority Key Identifier:
3A:1A:83:4F:F4:57:F3:E4:39:9C:33:00:48:76:8F:64:67:92:78:40
X509v3 Basic Constraints: critical
CA:FALSE
X509v3 Key Usage:
Digital Signature
X509v3 Subject Key Identifier:
48:4F:E9:2C:38:CF:01:EC:3C:EB:57:4E:CC:65:91:91:EF:F8:56:CA
Signature Algorithm: sha256WithRSAEncryption
Signature Value:
9d:54:ba:25:bd:c3:4a:55:6d:5c:7d:d4:d5:e5:9e:5d:10:55:
bf:55:25:37:99:49:f6:ed:5b:ef:53:f7:ec:a3:bb:a8:d3:a8:
5e:55:e9:3a:a2:5d:92:d1:5b:c1:69:8b:9b:26:e5:89:99:ae:
35:43:fd:ea:72:ef:d2:45:da:e7:9e:a0:44:85:4f:55:73:fb:
e9:7f:ec:75:47:c4:ba:de:55:d2:6c:65:51:ef:72:62:2a:2f:
5e:b5:7f:a4:99:28:c2:66:28:55:d5:77:19:ca:24:7e:7d:22:
c2:0c:64:d8:c4:fa:79:4b:bb:63:5c:7e:bc:35:46:7c:a7:32:
3d:38:35:e6:18:9d:d6:9a:0e:98:7a:59:14:fb:fc:23:8a:25:
6c:cd:91:18:05:89:92:62:82:39:f0:9a:33:c2:44:1b:bd:3e:
b7:4d:91:3a:3d:a2:67:9c:91:66:8e:e8:e1:14:52:2b:ea:d7:
df:f9:e2:4e:07:c3:b5:20:3a:7a:ae:c5:76:2c:06:67:a9:5c:
2d:8f:95:bf:00:9d:be:71:8c:9a:e6:c7:40:a6:88:8b:5e:e4:
d1:9e:24:df:60:02:89:ae:c6:f2:1c:9c:8e:ab:27:76:37:77:
68:91:56:8d:46:ab:79:e8:18:25:26:ac:ca:58:a9:53:01:de:
2f:ca:d9:59
Manually generating the (self) signature for the CA certificate
We have used openssl above to (self) sign the certificate, but I’d like to drill into the depths of what actually happened to generate this signature value.
From textbooks such as Understanding Cryptography by Christof Paar, Jan Pelzl & Tim Güneysu, wikipedia articles and similar, the text-book approach to RSA signing describes the following function (noting that I know enough to understand that there are insecurities in textbook RSA, but not yet knowing enough to understand what they are or why they arise - one for a later post);
\[signature = message^{privateKey}\bmod{N}\]Where;
- Signature is the value that will be added to the signed certificate in the
Signature Valuefield - message is some derivation of the certificate - predominantly containing the hash of relevant elements of the certificate
- privateKey is the value \(d\) of the private part of the key pair
- \(N\) is the RSA modulus from the key pair
I’d like to work through the process for signing to see if I can re-create this arithmetic operation and result at the same signature value as that generated by openssl.
I’ll do this in python, and will avoid meddling with asn1 and DER formats by utilising the x509 interface of the cryptography module - the keenformatics blog post is interesting as they take a different approach and manually extract the bytes from the DER representation of the certificate using dd after determining the offset and length by looking at the asn1 representation.
I’ll start off by importing the relevant modules to work with x509 certificates and create sha256 hashes, then read the CA pem certificate file and create a cert object. (note I’m being intentionally fast and loose with error handling etc. for brevity).
1
2
3
4
5
6
7
from cryptography import x509
from cryptography.hazmat.primitives import serialization
from hashlib import sha256
certificate = x509.load_pem_x509_certificate(open('dummyCA.pem', 'rb').read())
private_key = serialization.load_pem_private_key(open('CA-key.key', 'rb').read(), password=None)
We can access all the various aspects of data held within the certificate and private key here e.g.
1
2
print(certificate.subject)
print(private_key.key_size)
1
2
<Name(CN=dummyCA)>
2048
Specification of the signing algorithm
I’ve worked back from the x509 rfc5280 here to follow the chain of standards that clarifies how x509 certificates are signed
- The
signatureValuesection of rfc5280 refers to 3 separate rfc documents that describe various algorithms in use - Our dummyCA certificate has the string
sha256WithRSAEncryptionin thesignatureAlgorithmfield - from the 3 rfc’s listed in rfc5280, this algorithm is covered in rfc4055 - within rfc4055, our
sha256WithRSAEncryptionis listed within section 5, indicating that this algorithm uses the PKCS #1 V1.5 signature algorithm. This rfc refers to older rfc’s that contain the PKCS specifications - the newest updated rfc is ultimately rfc8017 which contains all the various PKCS algorithms spanning back to V1.5 - within rfc8017, section 8.2 details the steps required to generate an RSA signature, and refers internally to section 9.2 which details the PKCS#1 V1.5 encoding scheme
From rfc4055;
and from rfc8017;
Which part of the certificate is actually signed?
The entire certificate isn’t hashed as part of the signing process, rather a subset of the data referred to as the to-be-signed section - we can retrieve just this portion of the certificate data and obtain a sha256 hash;
1
sha256(certificate.tbs_certificate_bytes).hexdigest()
1
fa32d5df69aa2699e986689bc157d3df0aaf22589ad30852c06fa8e8d985f17e
Naively I assumed that the message used in the here would simply be the output of the sha256 hash, but there appear to be a variety of security property reasons that require the number of bits to be close to the size of the modulus here. This is where section 8.2 of rfc8017 comes in.
The PKCS #1 V1.5 encoding scheme
The section of rfc8017 describing the encoding scheme outlines that the digest of the message (in this case, the tbs_certificate_bytes value) is encoded into an ASN.1 value - I was about to reluctantly take a dive into ASN.1 to see if I could use python asn1 modules to perform this encoding based on the schema outlined in the standard, however I stumbled upon the notes section a few pages down which massively simplifies this exercise (and avoids the need to work out how ASN.1 and DER works to perform an encoding);
From the algorithm specification, we are looking to form;
1
EM = 0x00 || 0x01 || PS || 0x00 || T
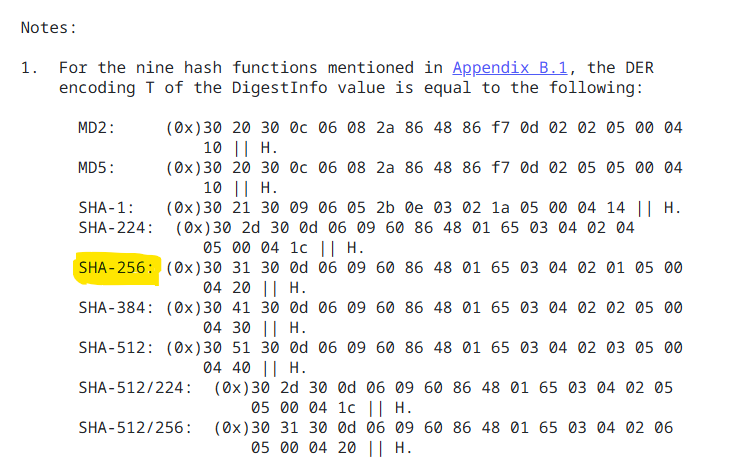
and from the notes for sha256 we know that;
1
T = 0x3031300d060960864801650304020105000420 || H
and we know H as we generated this above as sha256(certificate.tbs_certificate_bytes);
1
fa32d5df69aa2699e986689bc157d3df0aaf22589ad30852c06fa8e8d985f17e
Finally, we need to determine the length of the padding PS.
- the encoded message (EM) length = keylength, which is 2048 bits => 256 bytes
- T (see above) is 19 bytes in length + the 32 byte (256 bit) output of the sha256 hash => 51 bytes
- We add 2 bytes at the front of EM, and one between the padding and T => 3 bytes
- therefore, the padding length == 256 - 51 - 3 == 202 bytes (of 0xff)
We can now construct the encoded message
1
2
3
4
5
6
EM = bytearray(b'\x00\x01')
EM.extend(b'\xff' * 202)
EM.extend(b'\x00')
EM.extend(bytes.fromhex('3031300d060960864801650304020105000420'))
EM.extend(sha256(certificate.tbs_certificate_bytes).digest())
print(bytes(EM).hex())
1
2
3
4
5
6
7
0001ffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff
ffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff
ffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff
ffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff
ffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff
ffffffff003031300d060960864801650304020105000420fa32d5df69aa2699e986689bc157d3df
0aaf22589ad30852c06fa8e8d985f17e
Generating the signature
We can now raise the value of the encoded message (tbs_bytes of the certificate) to the power of the private key value \(d\), modulo the rsa modulus (obtained from the public key here as accessible with the cryptography module);
(For clarity, the python function pow(m,e,n) implements \(m^{e}\bmod{n}\). )
1
2
3
4
5
manual_signature = pow(int.from_bytes(EM),
private_key.private_numbers().d,
certificate.public_key().public_numbers().n)
print(format(manual_signature, 'x'))
1
2
3
4
5
6
7
74104c696d25472f960f75799bcc41a8477d69335f9a94c044b960b930fed55d0e1e40bd135b0ad3
ae38218c2b305f5951f904574b484fe71f6ba685445b3229209a2e971781686f7ba24854052d7412
b0f072fd3907a7b4b9bdc561cd213f9e5cc958f1a5a29197a944362c6c6750e6acd2dd459677a762
912ecfcd6ab1b4718ba232450e9caabce7e6098404437e3f46430f4b99f880d14fd1b4b7f01aa2d8
76c5e25775eb82a1f373d37740e4a374998c5fece0d452d7b4a589bfed5c13b48ef9a602c7f95af4
4a6fe55b8ed050273a98f3eb07a5ef9c160da840d0913e1a4ec7a1276642121111ec6d4c74d10257
d2a60498516af16613a50b8c21fd1238
This (as intended) matches exactly the signature that was generated by openssl when the self signed certificate was created
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
$ openssl x509 -in dummyCA.pem -text -noout -certopt ca_default -certopt no_validity \
-certopt no_serial -certopt no_subject -certopt no_extensions -certopt no_signame
Signature Algorithm: sha256WithRSAEncryption
Signature Value:
74:10:4c:69:6d:25:47:2f:96:0f:75:79:9b:cc:41:a8:47:7d:
69:33:5f:9a:94:c0:44:b9:60:b9:30:fe:d5:5d:0e:1e:40:bd:
13:5b:0a:d3:ae:38:21:8c:2b:30:5f:59:51:f9:04:57:4b:48:
4f:e7:1f:6b:a6:85:44:5b:32:29:20:9a:2e:97:17:81:68:6f:
7b:a2:48:54:05:2d:74:12:b0:f0:72:fd:39:07:a7:b4:b9:bd:
c5:61:cd:21:3f:9e:5c:c9:58:f1:a5:a2:91:97:a9:44:36:2c:
6c:67:50:e6:ac:d2:dd:45:96:77:a7:62:91:2e:cf:cd:6a:b1:
b4:71:8b:a2:32:45:0e:9c:aa:bc:e7:e6:09:84:04:43:7e:3f:
46:43:0f:4b:99:f8:80:d1:4f:d1:b4:b7:f0:1a:a2:d8:76:c5:
e2:57:75:eb:82:a1:f3:73:d3:77:40:e4:a3:74:99:8c:5f:ec:
e0:d4:52:d7:b4:a5:89:bf:ed:5c:13:b4:8e:f9:a6:02:c7:f9:
5a:f4:4a:6f:e5:5b:8e:d0:50:27:3a:98:f3:eb:07:a5:ef:9c:
16:0d:a8:40:d0:91:3e:1a:4e:c7:a1:27:66:42:12:11:11:ec:
6d:4c:74:d1:02:57:d2:a6:04:98:51:6a:f1:66:13:a5:0b:8c:
21:fd:12:38
Manually verifying the signature of the self-signed CA certificate
Verification of a signature follows the equivalent RSA encryption process, i.e.
\[message = signature^{publicKey}\bmod{N}\]Hence, when validating a certificate, the verifier;
- extracts the to-be-signed section of the certificate
- generates the \(message\) (that is, the PKCS #1 v1.5 encoded value of the sha256 hash of the to-be-signed section)
- extracts the \(signature\), publicKey \(exponent\) and modulus \(N\) from the certificate
- derives the expected message from this function and compares to the message obtained above
- if matched, the certificate signature is verified
As above, we start off by importing the relevant modules to work with x509 certificates and create sha256 hashes, then read the CA pem certificate file and create a cert object - this time I don’t use any elements of the private key - verification (understandably) takes place with the public certificate elements only.
1
2
3
4
from cryptography import x509
from hashlib import sha256
certificate = x509.load_pem_x509_certificate(open('dummyCA.pem', 'rb').read())
Generating the message value from the certificate
As above, we sha256 hash the to-be-signed section of the certificate;
1
sha256(certificate.tbs_certificate_bytes).hexdigest()
1
fa32d5df69aa2699e986689bc157d3df0aaf22589ad30852c06fa8e8d985f17e
And we follow the PKCS #1 v1.5 encoding scheme to construct the encoded message (as above)
1
2
3
4
5
6
EM = bytearray(b'\x00\x01')
EM.extend(b'\xff' * 202)
EM.extend(b'\x00')
EM.extend(bytes.fromhex('3031300d060960864801650304020105000420'))
EM.extend(sha256(certificate.tbs_certificate_bytes).digest())
print(bytes(EM).hex())
1
2
3
4
5
6
7
0001ffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff
ffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff
ffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff
ffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff
ffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff
ffffffff003031300d060960864801650304020105000420fa32d5df69aa2699e986689bc157d3df
0aaf22589ad30852c06fa8e8d985f17e
This is the value we aim to match.
Derive the expected message from certificate values
We can observe the public values from the certificate;
Signature
1
print(format(int.from_bytes(certificate.signature), 'x'))
1
2
3
4
5
6
7
74104c696d25472f960f75799bcc41a8477d69335f9a94c044b960b930fed55d0e1e40bd135b0ad3
ae38218c2b305f5951f904574b484fe71f6ba685445b3229209a2e971781686f7ba24854052d7412
b0f072fd3907a7b4b9bdc561cd213f9e5cc958f1a5a29197a944362c6c6750e6acd2dd459677a762
912ecfcd6ab1b4718ba232450e9caabce7e6098404437e3f46430f4b99f880d14fd1b4b7f01aa2d8
76c5e25775eb82a1f373d37740e4a374998c5fece0d452d7b4a589bfed5c13b48ef9a602c7f95af4
4a6fe55b8ed050273a98f3eb07a5ef9c160da840d0913e1a4ec7a1276642121111ec6d4c74d10257
d2a60498516af16613a50b8c21fd1238
Exponent
1
print(certificate.public_key().public_numbers().e)
1
65537
and modulus
1
print(format(certificate.public_key().public_numbers().n, 'x'))
1
2
3
4
5
6
7
a2790d9e1aa9824dcc333fdbbc43ab64e19b3ef392d0da18e08c8e73e8b093a7d7aedfd89229d4a0
50ca5e2ec56e6fc8358980b0a79d532d6424350891e09977482eda93f0ea253c5cdea8a2d5e6b2f3
a11568cea43726cfbbba4302d5ac7fa2433c8efb198905495507595c79b1b451f8d1d4b38773bdb3
9a9ce28eb576d50bb53fdf4bcf4b2f2dadfc7e0ae7b979ea20eccab60b83ed20e41a188319f57312
005fa87bb6f718863a31d33937d3ac370deaf0331edce174618b50707c0960d48f5468c5a64a1dd9
c605a795ace25cf459a7618626630a4f6e3976d4a134e75c8303d0a6fd276578a427910ebb7500f9
402332d148c76d319c0e9a9888e2689f
We can now raise the value of the signature to the power of the exponent e in the public key, modulo the modulus from the public key;
1
2
3
message = pow(int.from_bytes(certificate.signature),
certificate.public_key().public_numbers().e,
certificate.public_key().public_numbers().n)
And looking at these values side by side (note that as an integer, the leading 0x00 bytes are dropped);
1
2
3
print(format(message, 'x'))
print(bytes(EM).hex())
int.from_bytes(EM) == message
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
1fffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff
ffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff
ffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff
ffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff
ffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff
fffff003031300d060960864801650304020105000420fa32d5df69aa2699e986689bc157d3df0aa
f22589ad30852c06fa8e8d985f17e
0001ffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff
ffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff
ffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff
ffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff
ffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff
ffffffff003031300d060960864801650304020105000420fa32d5df69aa2699e986689bc157d3df
0aaf22589ad30852c06fa8e8d985f17e
True
We have verified that the signature on this self-signed certificate is valid
Manually verifying a signature of a certificate signed by this CA
From the dummyCA created in this post, we also generated and signed (with the dummyCA) an end-entity certificate - we can use this same process as above to verify the signature of this certificate.
Note that the exponent and modulus are taken from the CA certificate, with the to-be-signed and signature sections taken from the end-entity certificate;
1
2
3
4
5
6
7
ca_certificate = x509.load_pem_x509_certificate(open('dummyCA.pem', 'rb').read())
end_entity = x509.load_pem_x509_certificate(open('end-entity.pem', 'rb').read())
EM = bytearray(b'\x00\x01')
EM.extend(b'\xff' * 202)
EM.extend(b'\x00')
EM.extend(bytes.fromhex('3031300d060960864801650304020105000420'))
EM.extend(sha256(end_entity.tbs_certificate_bytes).digest())
This EM is the value we aim to calculate from the signature and CA cert modulus and exponent;
1
2
3
4
5
6
7
message = pow(int.from_bytes(end_entity.signature),
ca_certificate.public_key().public_numbers().e,
ca_certificate.public_key().public_numbers().n)
print(format(message, 'x'))
print(bytes(EM).hex())
int.from_bytes(EM) == message
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
1fffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff
ffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff
ffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff
ffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff
ffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff
fffff003031300d0609608648016503040201050004202ac6862657b100a9da325e45f5d7290f479
603ea522e0dd47269fd723e8099e8
0001ffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff
ffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff
ffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff
ffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff
ffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff
ffffffff003031300d0609608648016503040201050004202ac6862657b100a9da325e45f5d7290f
479603ea522e0dd47269fd723e8099e8
True
We have verified that the signature on this end-entity certificate was generated by the CA certificate
Verifying the let’s encrypt intermediate against the ISRG Root
In this post I used openssl s_client to obtain the wikipedia.com end-entity certificate and the let’s encrypt intermediate form the served certificate bundle.
The wikipedia.com end-entity certificate is signed using the ecdsa-with-SHA384 algorithm, so I can’t use this process to manually verify, but the let’s encrypt intermediate in the bundle is signed using sha256WithRSAEncryption so we can use our process to manually verify.
(Note that the ISRG Root X1 modulus is 4096 bits [512 bytes] long, so the padding needs an additional 256 bytes == 202 + 256 == 458 * 0xff)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
ca_certificate = x509.load_pem_x509_certificate(open('ISRG_Root_X1.pem', 'rb').read())
intermediate = x509.load_pem_x509_certificate(open('lets-encrypt-intermediate.pem', 'rb').read())
EM = bytearray(b'\x00\x01')
EM.extend(b'\xff' * 458)
EM.extend(b'\x00')
EM.extend(bytes.fromhex('3031300d060960864801650304020105000420'))
EM.extend(sha256(intermediate.tbs_certificate_bytes).digest())
message = pow(int.from_bytes(intermediate.signature),
ca_certificate.public_key().public_numbers().e,
ca_certificate.public_key().public_numbers().n)
print(format(message, 'x'))
print(bytes(EM).hex())
int.from_bytes(EM) == message
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
1fffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff
ffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff
ffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff
ffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff
ffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff
ffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff
ffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff
ffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff
ffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff
ffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff
ffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff
fffffffffffffffffffffffffffffffffffff003031300d060960864801650304020105000420f7f
5af28801e877d7df3a2be28fe149f3274a7ed29f136fd503ce398cba80b0d
0001ffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff
ffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff
ffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff
ffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff
ffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff
ffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff
ffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff
ffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff
ffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff
ffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff
ffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff
ffffffffffffffffffffffffffffffffffffffff003031300d060960864801650304020105000420
f7f5af28801e877d7df3a2be28fe149f3274a7ed29f136fd503ce398cba80b0d
True
We have validated that the signature on this let’s encrypt intermediate certificate was generated by the ISRG Root X1 certificate